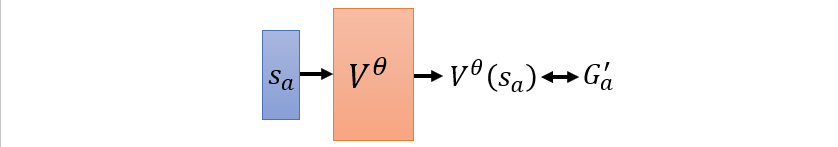Reinforcement learning

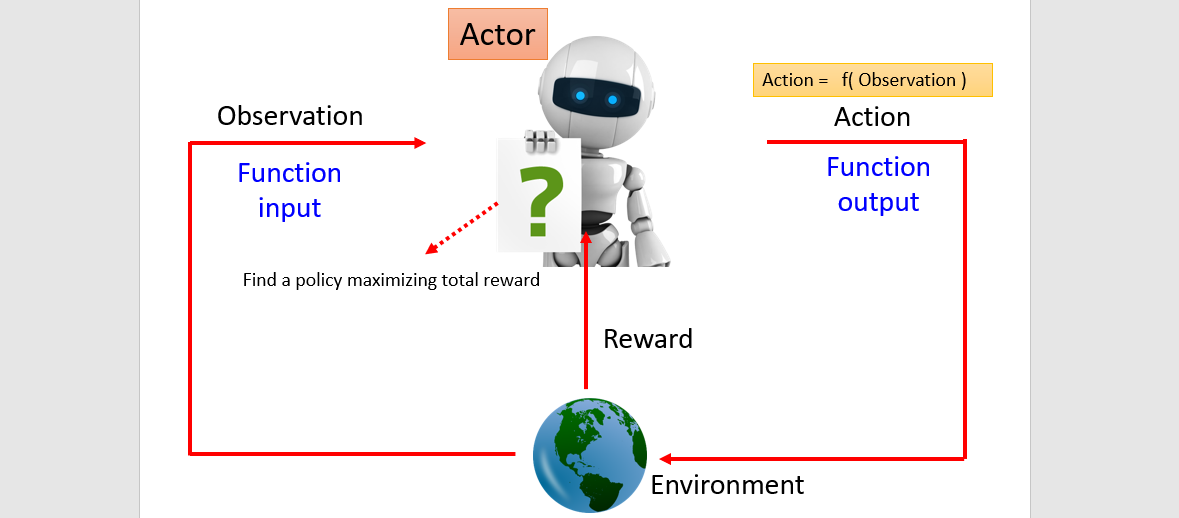
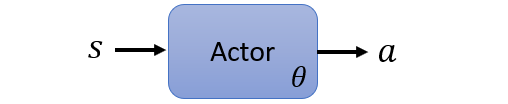
$S$: observation, $a$: action, $\theta$: parameter, $G$: cumulated reward, $\pi$: policy(network), $r$: reward

$\tau$: trajectory, $A^{\theta}(s_t, a_t)$: advantage function

$\tau = \{s_1, a_1, s_2, a_2, …, s_T, a_T\}$

$p_{\theta}(\tau) = p(s_1) \Pi p_{\theta}(a_t|s_t)p(s_{t+1}|s_t, a_t)$

$R(\tau) = \sum_{t=1}^Tr_t$ (random)

$\bar R_{\theta} = \sum_{\tau} R(\tau)p_{\theta}(\tau)$ (Expected Reward) cannot calculate → sampling

Reward delay: sacrifice immediate reward to gain long-term reward

• Cumulated reward

  Cumulated reward(based on distance)

  $G = \sum \gamma^{n-t} r_n$ ($\gamma < 1$)

• Policy gradient

  $\nabla \bar R_{\theta} = \sum_{\tau} R(\tau) \nabla p_{\theta}(\tau)$ $\nabla f(x) = f(x) \nabla \log f(x)$

  $\nabla \bar R_{\theta} = \sum_{\tau} R(\tau) p_{\theta}(\tau) \dfrac{\nabla p_{\theta}(\tau)}{p_{\theta}(\tau)}$

  $\nabla \bar R_{\theta} = \sum_{\tau} R(\tau) p_{\theta}(\tau) \nabla \log p_{\theta}(\tau)$

  $\nabla \bar R_{\theta} = \dfrac{1}{N}\sum_{n}^N\sum_{t}^{T_n} R(\tau) p_{\theta}(\tau^n) \nabla \log p_{\theta}(a_t^n|s_t^n)$

  $\theta^1 = \theta^0 + \eta \nabla \bar R_{\theta}$

  Add baseline to avoid always positive

  $\nabla \bar R_{\theta} = \dfrac{1}{N}\sum_{n}^N\sum_{t}^{T_n} (R(\tau) - b) p_{\theta}(\tau^n) \nabla \log p_{\theta}(a_t^n|s_t^n)$

  Assign suitable credit

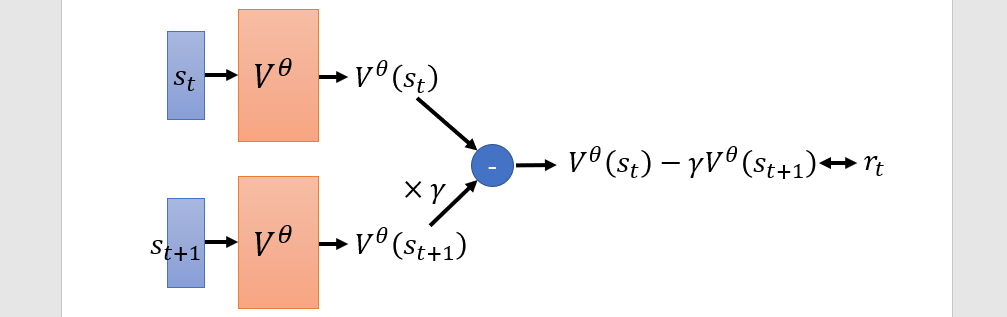
  $R(\tau^n) = \sum_{t^\prime}^{T_n} \gamma^{t^{\prime}-t}r_{t^\prime}^n$ discount factor $\gamma < 1$, futher the smaller impact

  • On-policy: an actor for training & interacting is the same

  • Off-policy: an actor for training & interacting is different

  • Proximal policy optimization(PPO)

  Exploration: the actor needs randomness during data collection

• Actor-critic

  Value function $V^{\theta}(s)$:

  • Monte-Carlo based approach(MC)

    

  • Temporal-difference approach(TD)

    ⋯$𝑠_𝑡,𝑎_𝑡,𝑟_𝑡,𝑠_{𝑡+1}$⋯

    $𝑉^𝜃 (𝑠_𝑡)=𝑟_𝑡+𝛾𝑟_{𝑡+1}+𝛾^2 𝑟_{𝑡+2}…$

    $𝑉^𝜃 (𝑠_{𝑡+1})=𝑟_{𝑡+1}+𝛾𝑟_{𝑡+2}+…$

    $𝑉^𝜃 (𝑠_𝑡 )=𝛾𝑉^𝜃 (𝑠_{𝑡+1})+𝑟_𝑡$

    

  $A_t = G_t^\prime - V^{\theta}(s_t)$

  $A_t = r_t +V^{\theta}(s_{t+1}) - V^{\theta}(s_t)$ $= Q^{\pi \theta} (s_t, a_t) - V^{\theta}(s_t)$

  Shared parameter

  

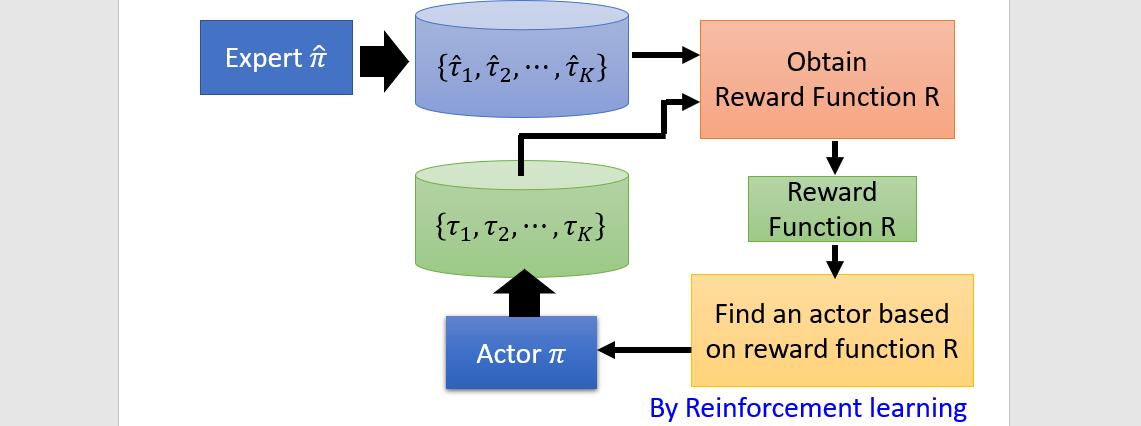
• Reward shaping

  Define extra reward to guide agents

  Curiosity based → see new meaningful things

• No reward

  Learn from demonstration

  • Imitation learning

  • Inverse reinforcement learning(IRL)

    $\sum R(\^\tau_n) > \sum R(\tau)$

    

    Actor → Generator, Reward function → Discriminator

• Q-learning

  $\mathbb E[G_t^n] = Q^{\pi \theta} (s_t^n, a_t^n)$

environment state: invisible to the agent

Specify the goal

$R(x) = -L(x)$

$L(x) = \sum A_n e_n$

• Agent state $S_t$

  a function of history. agent’s actions depend on state

  $S_{t+1} = u(S_t, A_t, R_{t+1}, O_{t+1})$

  • History: full sequence of observations, actions, rewards. Used to construct agent state.

  $H_t = O_0, A_0, R_1, O_1, …,$ $A_{t-1}, R_t, O_t$

  • Markov Decision Process: adding more history does not help.

    $S_t$ = $O_t$ = Environment state (sees everything)

  💡

  t: time step
  
  u(): state update function

  • Last observation: $S_t = O_t$ (not enough)

  • Complete history: $S_t = H_t$ (too large)

  • A generic update: $S_t = u(S_{t-1}, A_{t-1}, R_t, O_t)$

• Policy

  define agent’s behavior. $S_t → A_t$

  Deterministic policy: $A = \pi(S)$

  Stochastic policy: $\pi(A|S) = P(A|S)$

• Value functions

  select between actions, evaluate desirable state.

  $v_{\pi}(s) = \mathbb{E}[G_t | S_t = s, \pi]$
  
  $= \mathbb{E}[R_{t+1} + \gamma R_{t+2} + (\gamma)^2 R_{t+3} + … | S_t = s, \pi]$

  • Depends on policy

  • Recursive form $G_t = R_{t+1} + \gamma G_{t+1}$
    • Bellman equation

      $v_{\pi}(s) = \mathbb{E}[R_{t+1} + \gamma G_{t+1} | S_t = s, A_t = \pi(s)]$

      $= \mathbb{E}[R_{t+1} + \gamma v_{\pi}(S_{t+1}) | S_t = s, A_t = \pi]$

  💡

  discount factor $\gamma \in [0, 1]$
  immediate vs long-term
  rewards trade-off

• Model

  Predict what the environment will do next

  • $\mathcal{P}$ predict next state:

    $\mathcal{P}(s, a, s’) \approx p(S_{t+1} = s’ | S_t = s, A_t = a)$

  • $\mathcal{R}$ predict next (immediate) reward:

    $\mathcal{R}(s, a) \approx \mathbb{E}[R_{t+1} | S_t = s, A_t = a]$

• categories

  • Value based: value function

  • Policy based: policy

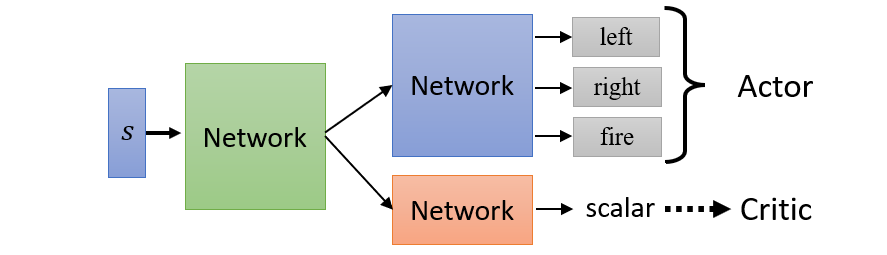
  • Actor critic: value function + policy

  • Model free: No model

  • Model based: model

  • Learning: environments are initially unknown

  • Planning: environments are known

  • Prediction: predict the future

  • Control: optimize the future